자바스크립트가 숫자데이터를 저장하는 방식 // 64비트 부동소수점
# deepdive에는 없는 내용이다
공부를 하다가 메모리에는 데이터가 2진법의 수로 저장이 된다고 하는데, 숫자데이터는 8바이트, 즉 64비트(1바이트=8비트)로 저장이 된다고 하였다.
그럼 2의 64승가지의 데이터가 저장이 될 수 있다는 말인데, 이렇게 많은 데이터를 표현할수 있는 공간은 어떻게 숫자를 표현할까? 라는 생각에 포스팅을 쓰게되었다.
# 자바스크립트 deep dive에서 표현한 방식
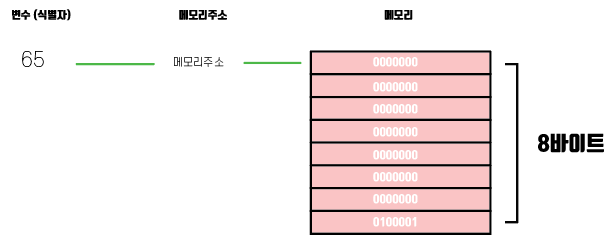
딥다이브에선 숫자가 이렇게 저장이 된다고 하였는데 물론 집필자쌤도 이건 그냥 예시라고 하였다.
그리고 64비트 부동소수점 방식으로 저장이 된다고 하였는데 사실 저 그림만봐도 맨아래 1바이트 공간빼고 나머지는 걍 다 0으로 채워져있어서 가성비 한남충인 나로써는 저 공간들이 너무 아까웠고 이해를 못하고 넘어가는게 답답해서 이 포스팅을 쓰기로 한거다..
아 지금다시보니 내가 0을 8개가아닌 7개로 적어놨다.. ㅈㅅ..
# 그렇다면 찐!!자바스크립트는 65라는 숫자를 어떻게 저장할까?
일단 그림으로 보여주겠다.

65라는 숫자는 이렇게 8바이트의 공간에 저장이 된다.
이게 뭐지?라는 생각이 들것이다ㅋㅋ
## 64비트 부동소수점 방식의 8바이트 공간 활용
# 숫자데이터가 저장되는 공간 8바이트!
숫자값이 저장되는 8바이트의 공간은 총 비트수로 생각하면 64비트이다.
1바이트가 8비트이니 말이다.
이 비트에는 0이나 1이 저장될수 있다. 그냥 불린처럼 모아니면도 라는 두가지 데이터가 저장이 된다는 것이다.
그러니 이름도 '64비트' 부동소수점 방식일꺼다..
암튼 숫자데이터 하나를 저장하는데 64개의 비트가 활용된다는 것이다.

이 그림에서 네모 한칸이 1비트이다.
사람은 10진법을 좋아하니 네모 10칸씩 가시적으로 표현했는데 그냥 저 공간은 쭉 이어붙어져있다.
그럼 자바스크립트가 사용하는 64비트 부동소숫점 방식은 이 64개의 비트공간을 어떻게 활용할까?
# 총 64비트의 공간은 비트부호, 지수부, 가수부로 활용된다

위 그림에 색깔을 넣어서 구분해봤다.
총 64개의 비트는 순서대로
비트부호( 1비트 )
지수부 ( 11비트 )
가수부 ( 52비트 )
로 사용된다.
# 비트부호 (1비트)
처음 선두셀인 비트부호는 총 1비트의 데이터 공간을 가지고있다.
1비트에는 0이나 1만 저장될수있어서 이 1비트의 공간으로 저장될수 있는 데이터는 총 2가지다 ㅋㅋ
이 공간은 양수냐 음수냐를 저장하는데 0이저장되면 양수, 1이 저장되면 음수라는 뜻이다.
뭐 하긴 10이나 -10이나 부호하나차이니 1비트면 충분하긴하다.
아 참고로 0은 음수도 양수도 아닌데.. 어떻게될지 궁금하긴한데 이미 엘리스의 토끼굴에 깊게 들어와버렸으니 스킵하겠다
# 지수부 (11비트)
지수부는 11비트의 공간을 가지고 있다.
데이터는 총 2^11인 2048개가 저장될 수 있다.
이 공간의 활용은 사실 어떻게 설명할지 잘 감이 안잡히는데 대충 설명하자면
10진법 숫자를 2진법으로 바꾼후, 이 숫자를 정규화를 한다.
정규화를 하면 이 숫자를 1.01010101 * 2의 몇승으로 표현가능한데 여기서 2의 몇승 부분인 지수가 이 11비트에 저장이 된다.
# 가수부 (52비트)
가수부는 52비트나 가지고있다! 데이터는 2^52개가 저장될수 있는 공간이다.
위에 지수부에서 설명했듯이 숫자를 2진법 수로 바꾸고 정규화를 하면 1.머머머머 * 2의 몇승 으로 표현가능한데 여기서 '머머머머'부분을 가수부 공간에 채운다.
사실 여기까지 설명을 들으면 뭔 개소리인가 싶을거다..
그래서 시작하자마자 숫자 65를 저장한 메모리공간 그림을 보여줬는데
이 숫자로 예시를 들어보겠다.
# 실전! 10진법 숫자가 메모리공간에 저장되는 데이터 계산해보기.
1, 비트부호.
65는 양수다. 위에 설명했듯이 음수면 1 양수면 0이되는데 65는 양수니까 0이 저장될거다

* 여기서 잠깐! 지수부와 가수부를 설명하기 전에, 숫자를 정규화를 먼저 해야한다.
65라는 숫자를 메모리공간에 64비트 부동소수점방식으로 저장하기 위해서는
설명했듯이 비트부호 지수부 가수부로 나누어야 한다.
- 65라는 숫자를 먼저 2진법 수로 바꿔보자. 바꾸면 1000001이 된다.
콘솔에 0b붙이고 이거 써보면 65나온다.
console.log(0b1000001); //65뜸- 그럼 이 이진법수 1000001을 1.소숫점 머머머 * 2의 몇승 으로 표현해보자
1.000001 * 2^6이 될것이다. 이게 정규화한거다.
2. 가수부
가수부는 52칸이나 되는 무지막지한 공간을 가지고있지만 걍 단순하다.
위에 정규화를 한 식에서 소숫점부분(.000001)을 순서대로 걍 채워 넣는다.

이렇게 된다
3. 지수부
지수부가 조금 까다로운데 저 정규화 한 부분에서 2의 몇승인 부분을 저장해야하는 곳이다.
65를 정규화한거에서 2의 6승의 이 '6'이 지수부분에 사용할 부분이다.
근데 이 6을 2진법으로 변환한 110으로 채우는게아니라, 1023+6인 1029를 2진법으로 바꾼 10000000101을 집어넣는다.
여기서 1023을 bias라고하는데 기준점을 나눈거다.
* bias란?
음수와 양수로 표현될 수 있는 부분을 전부 양수로 끌어올린거다.
데이터베이스? 이런데서 좀 봤었는데, 메모리에는 음수를 표현할 수 없다.
예시를 들어보자면
65숫자의 지수부 10진법 숫자 6을 그냥 2진법 데이터 00000000110로 채운다고 한다면,
반례로 10진법 숫자 0.25를 저장하는걸 생각해보자.
10진법 숫자 0.25를 2진법으로 바꾸면 0.01이다.
이걸 정규화한다면
1 * 2^(-2)이 되는데 이 -2를 2진법 데이터로 바꾸면 -10이다.
이걸 지수부에 저장하려면 음수인데? 어케함? 또 부호정해줘야하는데..?
방법이 없을거다.. 그래서 이렇게 최소음수부분을 0부터 시작하게하고, 음수와 양수의 기준점을 정한게 bias 기준점이다.
따라서 이 '몇승'이 양수라면 10000000000보다 큰 수가 지수부에 들어갈테고,
이 '몇승'이 음수라면 10000000000보다 작은수가 들어갈것이다.(01111111111이런식)
최종적으로
저 1029를 2진법데이터로 바꾼 10000000101을 지수부에 넣으면 된다.
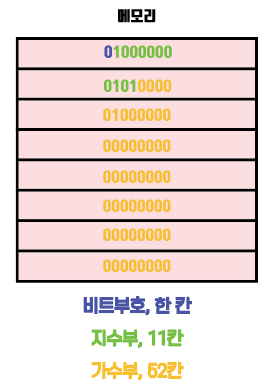
이렇게 최종적으로 65라는 10진법 숫자가 메모리상에 64비트부동소수점방식으로 저장이 된다.
## 자바스크립트 숫자데이터 터뜨리기!
재밋는 짓을 좀 해보자 (나만 재밋을수도..)
# 지수부 데이터 터뜨리기.
위에서 설명한바로 지수부에는 11비트가 할당되는데, 만약에 11비트가 넘는 데이터가 들어간다면
자바스크립트가 숫자를 표현하지 못하지 않을까?
먼저 일단 비트부호를 양수로 할거고, 가수부는 신경을 안 쓸 생각이다.
그렇다면 가장 좋은 방법은 2의 n제곱인 정수를 넣어보는것이다.
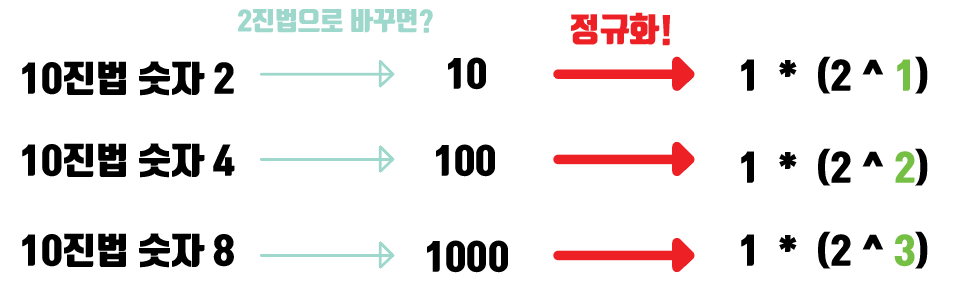
이렇게 보다시피 2의 n제곱 정수는 가수부가 그냥 다 00000~(52개)로 구성된다
그리고 정규화를 했을때 지수 부분이 10진법숫자의 n승의 숫자랑 같아진다.
아까 지수부분은 11비트로 이루어진다고 하였다.
이 11비트의 공간에는 2의 11승인 2048가지의 데이터가 저장된다.
그럼 이 지수부분에 저장될수 있는 2048가지의 경우의수를 초과한 경우를 만들어보면 자바스크립트는 못읽겠지?ㅋㅋ
아까 65를 정규화하는 과정에서 저 지수(승)부분이 6이 나왔다.
bias숫자 1023+6을 2진법으로 바꿨었었고, 그 2진법 데이터가 10000000101이었다.
그럼 이렇게 나온 2진법데이터가 11111111111(11개)이 되는경우가 어떻게 될까?
만약 11개를 넘어선 12개가 되는순간의 숫자는 뭘까?
역순으로 계산해보면, 2진법수 11111111111(11개)는 10진법수로 2047이다. (2의 11승에서 1뺀값)
이 숫자 2047에 bias숫자 1023을 뺴보면 1024이다.
즉 10진법 숫자 2의 1024승이 자바스크립트에서 지수부분의 최댓값 수이다.
콘솔로 쳐보자.
console.log(2 ** 1023); // 뭐시기 나옴
console.log(2 ** 1024); // infinity
console.log(2 ** 1025); // infinity2의 1023승은 숫자로 뭔가 나오긴한다 ㅋㅋ 워낙 큰수니까 뭐..
근데 1024승부터는 그냥 무한대로 표현을 한다.
난 기댓값으로 2의 1024까지는 나올줄 알았는데 자바스크립트는 2의 1024승부터 그냥 무한대 취급해버리는것같다.
! 여기서 주의할점은 2의 1024승이 자바스크립트에서 최대 숫자는 아니라는거다.
예시로
만약 2의 1024승 -1인 숫자도 가수부분이 터져버려서 계산이 터지긴 한다
또한 2의 1023승 -1인 수도 가수부분이 터져버려서 계산이 븅신같이된다.
예시를 보여주자면
let byungsin_num_1 = 2 ** 1023;
console.log("병신숫자1 : ", byungsin_num_1);분명 병신숫자는 콘솔로 찍혀진다! 지수부분 터뜨린 2의 1024승이 아닌 2의 1023승이기 때문이다.
콘솔로 병신숫자 1을 찍어보면

못생겼지만 이렇게 분명히 꾸역꾸역 뱉어낸다.
그럼 여기서 병신숫자 1과 '분명히'다른 병신숫자 2를 만들어보자.
let byungsin_num_1 = 2 ** 1023;
let byungsin_num_2 = 2 ** 1023 + 1;
console.log("병신숫자2 : ", byungsin_num_2);분명히 분명히 분명히!! 저 숫자 두개는 다르다. 1을 더했기떄문에 다른 숫자이다.
병신숫자 2를 콘솔로 찍어보면

이렇게 얘도 콘솔로 자바스크립트가 표현해준다.
근데 여기서 이상하게 느낀사람이 있을것이다.
병신숫자 1과 병신숫자 2가 참조값이 비슷하게 생겼다?
나도 첨엔 에이 숫자가 너무 크니 그런거겠지 했는데.. 자세히보니 똑같이 생겼다.
그래서 이 병신숫자 1과 2가 서로 같은지 찍어봤는데
console.log(
"이 병신 숫자 두개는 서로 같을까? : ",
byungsin_num_1 === byungsin_num_2
); // ㄷㄷ true래..이거 트루 뜬다..
이유는 가수부분도 터져버렸기 때문이다ㅋㅋㅋ
저렇게 큰 2의n승 +-1인 숫자는 가수부도 엄청 나게 길다.
10진법 숫자가 2의 정수 n승일떄 n값이 무지막지하게 큰데 이 2의n승에서 1을 더하고 뺀건 가수부분이 완전 난장판이 된다.
( 10진법수 2의 1023승의 가수부는 0000~~이지만 여기서 1만뺴도 000000000000000000~~~존나많이나온다 )
그런데 가수부에는 52자리까지 저장이 되기때문에 그냥 저기서 52자리까지만 메모리에 저장을 해놓는다.
그래서 저 일치연산자가 병신숫자 2개가 서로 같다고 하는거임.
# 가수부 데이터 터뜨리기.
물론 지수터뜨리기에서 2^1023 -1로도 가수를 터뜨려봤는데,
가수부 터뜨려보는건 사실 간단하다. 2진법에서 무한소수 나오는 숫자 쓰면되기때문이다.
다른 블로그 포스팅 보면 많이들 예시로 봤겠지만
10진법 숫자 0.1과 0.2는 2진법숫자로 무한소수가 된다.
console.log((0.1).toString(2));
console.log((0.2).toString(2));여기서 .toString(n)메서드는 앞에 숫자를 n진법 숫자로 바꿔줘~ 라는거다.
암튼 콘솔 결과를 보면

이렇게 2진법의 무한소수가 나온다. 계속 반복되지만 걍 저기쯤에서 끊어서 보여준다.
그럼 저 숫자들은 정규화했을때 가수부분이 52개의 데이터를 넘겨버린다. (당연히 무한히 반복되니..)
때문에
console.log(0.1 + 0.2);이런 코드를 쳐보면
콘솔에

이렇게 병신숫자 3이 나오게된다.
자바스크립트에선 숫자계산을 최대한 정수로 만들어내는게 좋을것같다.
예를들어 0.1+0.2 이렇게하지말고
(0.1 * 10 + 0.2*10)/10 이런식으로.. 그럼 제대로 뱉는다. 모던자바스크립트에서도 나와있는 방법이다.
아니면 다른 숫자계산 라이브러리가 있다고하는데 난 그냥 숫자계산할때는 파이썬 써야겠다..